梯度下降法的原理和公式这里不讲，就是一个直观的、易于理解的简单例子。

1.最简单的情况，样本只有一个变量，即简单的（x，y）。多变量的则可为使用体重或身高判断男女（这是假设，并不严谨），则变量有两个，一个是体重，一个是身高，则可表示为(x1,x2,y),即一个目标值有两个属性。

2.单个变量的情况最简单的就是，函数hk(x)=k*x这条直线(注意：这里k也是变化的，我们的目的就是求一个最优的   k)。而深度学习中，我们是不知道函数的，也就是不知道上述的k。   这里讨论单变量的情况：

在不知道k的情况下，我们是通过样本(x1,y1),(x2,y2)，(xn,yn)来获取k。获取的k的好坏则有损失函数来衡量。

损失函数：就是你预测的值和真实值的差异大小（比如一个样本（1，1）他的真实值是1，而你预测的是0.5，则差异   比较大，如果你预测值为0.9999，则差异就比较小了）。

损失函数为定义如下（此处为单变量的情况）

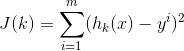
目的是求使损失函数最小的变量k（注意和变量x区分），则将损失函数对k求导（多变量时为求偏导得梯度，这里单变量求导，其实不算梯度），求偏导如下：

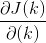
然后迭代，迭代时有个步长alpha,(深度学习中貌似叫学习率)

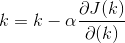
3.例子

假如我们得到样本(1,1),(2,2),(3,3).其实，由这三个样本可以得到函数为y = 1*x。此时损失函数为0.而机器是不知道的，所以我们需要训练。

下面是一段python代码。

import numpy as np
import matplotlib.pyplot as plt
x=np.arange(-5, 5, 0.001)
y=(((x-1)*(x-1)+(x*2-2)*(x*2-2)+(x*3-3)*(x*3-3))*1/6.0)
plt.plot(x,y) 
#plt.show() #显示图形 
 

def sum(x):
 return ((x*1-1)*1+(x*2-2)*2+(x*3-3)*3)
def fun(x):
 return ((1/3.0)*sum(x))
old = 0
new = 5
step = 0.01
pre = 0.00000001
 
def src_fun(x):
 print(((x-1)*(x-1)+(x*2-2)*(x*2-2)+(x*3-3)*(x*3-3))*1/6.0)
 
while abs(new-old)>pre:
 old = new
 #src_fun(old)  #输出每次迭代的损失值
 new = new - step*fun(old)
 
 
print(new)
print(src_fun(new))

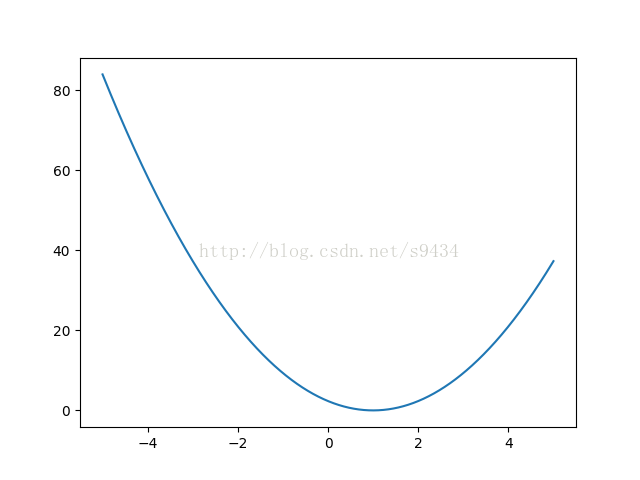
下图是损失函数的图像，损失函数中变量是k。下图横坐标为k的不同取值，纵轴为对应的损失大小。由下图可以大致看出，当k为1时，损失函数值为0。注意：这里取的最优值k=1是在我们已有样本的情况下得出的,样本不同，k值自然不同。

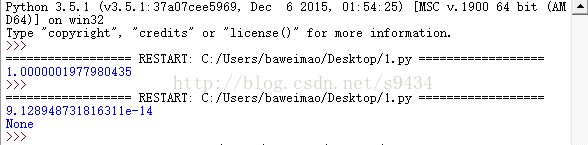
下面是print(new)和print(src_fun(new))的输出结果

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持【听图阁-专注于Python设计】。