python实现dijkstra最短路由算法
Dijkstra算法:又称迪杰斯特拉算法,迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止百度百科。
注意:Dijkstra算法不能处理包含负边的图
# dijkstra算法实现,有向图和路由的源点作为函数的输入,最短路径最为输出
def dijkstra(graph,src):
# 判断图是否为空,如果为空直接退出
if graph is None:
return None
nodes = [i for i in range(len(graph))] # 获取图中所有节点
visited=[] # 表示已经路由到最短路径的节点集合
if src in nodes:
visited.append(src)
nodes.remove(src)
else:
return None
distance={src:0} # 记录源节点到各个节点的距离
for i in nodes:
distance[i]=graph[src][i] # 初始化
# print(distance)
path={src:{src:[]}} # 记录源节点到每个节点的路径
k=pre=src
while nodes:
mid_distance=float('inf')
for v in visited:
for d in nodes:
new_distance = graph[src][v]+graph[v][d]
if new_distance < mid_distance:
mid_distance=new_distance
graph[src][d]=new_distance # 进行距离更新
k=d
pre=v
distance[k]=mid_distance # 最短路径
path[src][k]=[i for i in path[src][pre]]
path[src][k].append(k)
# 更新两个节点集合
visited.append(k)
nodes.remove(k)
print(visited,nodes) # 输出节点的添加过程
return distance,path
if __name__ == '__main__':
graph_list = [ [0, 2, 1, 4, 5, 1],
[1, 0, 4, 2, 3, 4],
[2, 1, 0, 1, 2, 4],
[3, 5, 2, 0, 3, 3],
[2, 4, 3, 4, 0, 1],
[3, 4, 7, 3, 1, 0]]
distance,path= dijkstra(graph_list, 0) # 查找从源点0开始带其他节点的最短路径
print(distance,path)
节点的遍历过程如下:
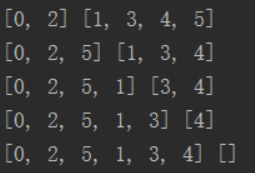
最短路径输出:

以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持【听图阁-专注于Python设计】。